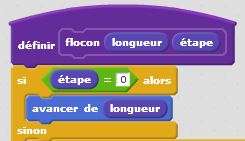
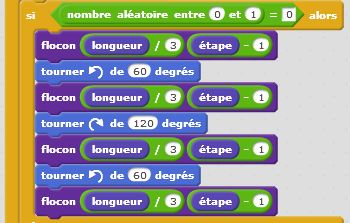
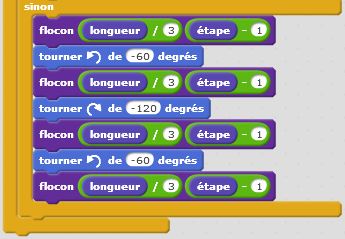
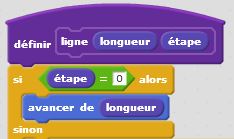
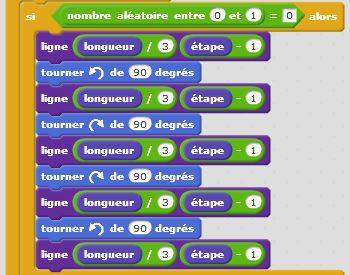
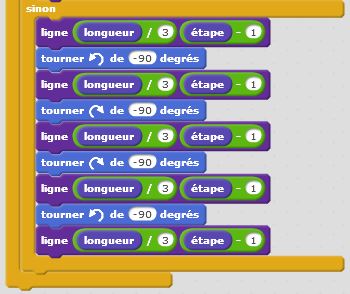
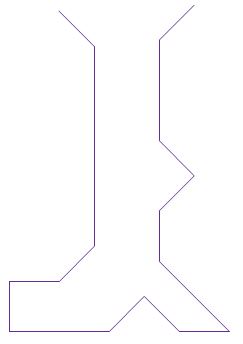
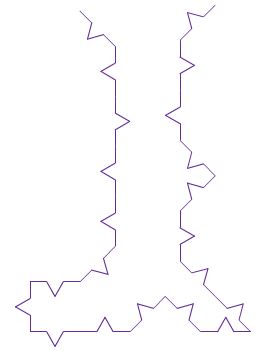
Introduisons l’aléatoire dans nos motifs fractals. Repartons du flocon de Von Koch et lançons une pièce bien équilibrée. Lorsqu’elle tombe sur pile, on place la pointe du triangle à l’extérieur, lorsqu’elle tombe sur face, on place la pointe du triangle à l’intérieur. Le « bien équilibrée » signifie que l’on a autant de chance de tomber sur pile que sur face. Techniquement, rien de plus simple : pour simuler « Pile » ou « Face » avec un ordinateur, on tire au hasard un nombre entier compris entre 0 et 1. Lorsqu’on obtient « 0 » cela correspond à « Pile ». Lorsqu’on obtient « 1 » cela correspond à « Face ». Tout langage de programmation intègre cette instruction parfois appelée « ALEA », mieux connue par les anglicistes sous le nom de « RANDOM ». Ensuite, en fonction du résultat obtenu, « 0 » ou « 1 », « Pile » ou « Face », nous changeons les angles de déplacement en leurs opposés ! Rien de plus simple… Et les résultats obtenus sont étonnants. Nous cassons la belle régularité et auto similarité de notre motif fractal et introduisons la notion de chaos dans cet ensemble bien ordonnée. Regardez ce que cela donne dans le cas du triangle de Von Koch puis dans le cas du carré de Von Koch… Surprenant, non ?
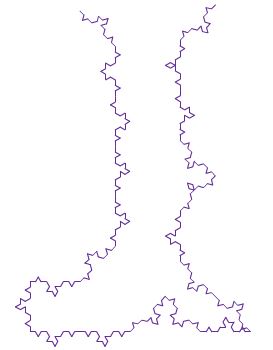
L’introduction du chaos dans les motifs fractals bien ordonnés a un intérêt : ils nous permet de coller de manière plus fidèle à la réalité. Le contour d’une ville n’aura jamais la forme du flocon de Von Koch, il se rapprochera plus facilement d’un fractale perturbée par le jet d’une pièce. Appliquons cette idée au contours d’un pays. Choisissons l’Italie. Nous ébauchons la péninsule à l’aide de quelques segments bien choisis. Chaque segment est substitué par une fractale de Von Koch. Bien entendu chaque segment ne sera pas substitué par la « même » fractale. Ayant pour chaque segment jeté au préalable une pièce, certains auront une pointe qui « sort » vers l’extérieur tandis que d’autres auront une pointe qui « rente » vers l’intérieur. Tout ceci de manière parfaitement aléatoire et donc chaotique. Répétons de manière itérative le processus pour chaque nouveau segment et observons ce qu’il se passe… Quand nous vous disions que le chaos nous permet de nous rapprocher de la réalité !
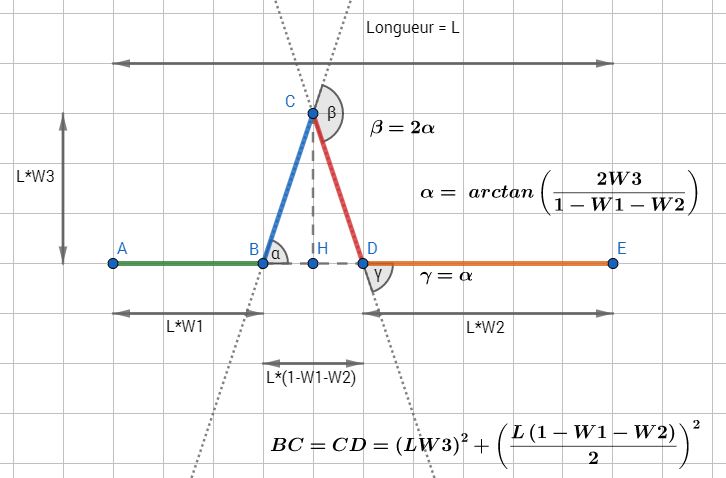
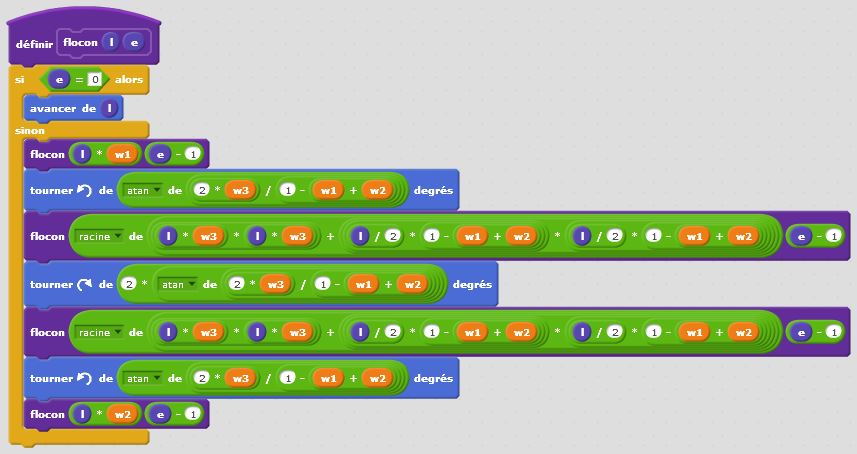
Pour terminer cet exposé, nous aimerions avoir une certaine maîtrise du chaos. Nous reprendrons notre motif fractal de base, le flocon de Von Koch. Cependant, au lieu de construire systématiquement le triangle équilatéral suivant au tiers du segment précédent, nous introduisons trois paramètres W1, W2 et W3 (trois nombres compris entre 0 et 1). Le premier, W1, correspond à la proportion du segment précédent que nous allons « laisser à gauche ». Le deuxième, W2, correspond à la proportion du segment précédent que nous allons « laisser à droite ». Le troisième, W3, correspond à la proportion du segment précédent que nous allons prendre comme « hauteur du pic » qui de ce fait, perd son statut de triangle équilatéral pour rejoindre celui de triangle isocèle. Programmer l’algorithme de construction de ce flocon paramétré requiert de solides connaissances en trigonométrie. Auparavant, le bloc « j’avance, je tourne, j’avance, je tourne, j’avance, je tourne, j’avance » se basait sur des longueurs élémentaires (le tiers des longueurs précédentes) et sur des angles remarquables (60°, ses multiples et/ou leurs opposés). Dans le cas présent, les paramètres W1, W2 et W3 viennent rompre cette douce régularité et perturber cette rigoureuse symétrie. Les paramètres W1 et W2 interviennent directement dans l’expression des deux longueurs initiales et finales. Le théorème de Pythagore permet de calculer la longueur des deux côtés du « pic ». La notion d’arc tangente nous permet de déterminer les trois angles « alpha », « beta » et « gamma » dont nous avons besoin pour tourner. Nous pouvons désormais nous reposer et profiter du spectacle. Tirons aléatoirement trois paramètres W1, W2 et W3 et observons toute la palette de combinaisons possibles. Étonnant non ?
 |