La collaboration entre le Lycée français Jean Giono de Turin et le Collegio Carlo Alberto de Moncalieri permet depuis plusieurs années à nos jeunes collégiens et lycéens de vivre les mathématiques selon les principes de la recherche dans le cadre d’un atelier Math en Jeans. Les travaux des élèves sont encadrés par Vivien Douine responsable du projet et sont supervisés par notre chercheur référent Guillaume Kon Kam King. Nous sommes heureux, de partager ci-dessous les sujets proposés aux élèves et dans les pages liées les résultats de nos recherches. Bonne lecture !

Les villes se développent seloxn deux grands types de mécanismes, soit elles suivent un schéma planifié souvent organisé autour de formes géométriques comme la grille ou les cercles concentriques, soit elle croissent de manière organique sous les contraintes géologiques (montagnes, fleuves) et des forces d’attraction générées par les marchés ou les lieux d’échanges, les grandes voies de transport, les gares etc. Dans son livre Fractal Cities Michael Batty explique que pour autant, jusqu’au début des années 80, seule la conception géométrique et planifiée de la croissance des villes a prévalu, occultant tout un pan de la réalité pourtant connu par les économistes et les sociologues. Entre les deux grands mécanismes, la formation des villes résulte de l’interaction entre une volonté de planification à l’échelle du centre ville et la somme d’une multitude de décisions individuelles locales corrélées. Les concepts classiques d’esthétique et de géométrie euclidienne qui jouent un rôle central dans l’étude du développement des villes sont peu adaptés à la description des structures émergeant de ces interactions, et nous aveuglent à une partie des phénomènes en jeu. En revanche, Michael Batty propose de profiter de l’émergence des sciences du chaos et de la complexité, ainsi que de la géométrie fractale qui fournit un langage dans lequel décrire les processus complexes et chaotiques et les outils pour les visualiser. L’objectif de ce projet sera de se familiariser avec les concepts fondamentaux liés à la géométrie fractale, puis d’étudier des modèles de croissance de ville utilisant des objets fractals. Il inclura une partie conséquente de programmation informatique. Cliquer sur l’image pour lire la suite…
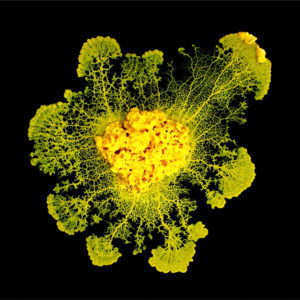
Le Blob est un être étrange, entre animal, végétal, champignon. Unicellulaire, c’est surtout une sorte de moisissure qui prospère dans les sous-bois sur les vieux troncs et les feuilles tombées au sol. On ne compte plus ses prouesses, qui vont de la survie en milieu hostile (eau, feu) à la cicatrisation en l’espace de quelques minutes, et même jusqu’à la duplication en cas de découpage. Il se régénère à intervalles réguliers, en séchant pour quelques jours avant de reprendre vie comme si le temps n’avait pas de prise sur lui. Le talent bien particulier qui va nous intéresser ici est la capacité du blob à se déplacer de manière très efficace pour récolter de la nourriture. Le blob s’étend pour couvrir une surface maximale, puis se concentre et fond pour ne garder que les axes les plus utiles pour faire circuler la nourriture dans son corps. Des chercheurs japonais on étudié plus précisément ce mode de déplacement et ont conclu qu’il constituait une méthode d’optimisation spatiale très performante, et proche d’autres structures de réseaux optimisés comme le métro de Tokyo . Ils présentent un modèle mathématique de formation de réseau inspiré de la biologie du blob que l’on étudiera et que l’on cherchera à simuler. Le principe de ce modèle est que partant d’un espace couvert de blob, des canaux se forment qui ont tendance à croître ou à décroître selon leur utilité pour transporter la nourriture. Le système évolue et lorsqu’il s’arrête, il atteint une structure presque optimale du point de vue de l’énergie dépensée et de la robustesse à des modifications suites à des dommages causés au blob. Cliquer sur l’image pour lire la suite…

Le sujet How the crocodile got its stripes, formation de motifs sur des supports dilatants vient prendre la suite du sujet sur la formation des motifs sur les pelages des animaux. Pour résumer, l’apport principal du modèle de Turing est d’expliquer comment des hétérogénéités peuvent s’établir dans un système où a lieu une diffusion. Cela peut expliquer un grand nombre de phénomènes, allant du pelage des léopards à la forme d’algues marines en passant par les motifs des ailes de certains papillons. Une conséquence particulièrement profonde de ces travaux est que la structure exacte des motifs n’est pas écrite dans le code génétique, ce qui demanderait d’y stocker beaucoup d’informations, mais se développe de manière aléatoire selon la température initiale et d’autres paramètres pour former un pelage distinctif mais unique (comme les empreintes digitales). Or il existe des situations où une difficulté supplémentaire s’ajoute au mécanisme de formation des structures. Par exemple, on sait que le nombre de rayures d’alligators du Mississipi dépend de la température à laquelle l’embryon se développe, et ceci pour des différences de températures trop faibles pour que l’on puisse puisse l’expliquer simplement par des vitesses de diffusion ou de réaction modifiée. En revanche, la taille de l’embryon dépend elle de manière très sensible de la température, et on peut faire l’hypothèse que c’est le développement de l’embryon qui conditionne le nombre de rayures. On s’intéresse particulièrement aux alligators parce qu’ils offrent des possibilités d’étude très intéressantes: on peut enlever la coquille de l’oeuf sans percer la peau et regarder l’embryon se développer, pour suivre au cours du temps la formation des motifs. Deux objets d’étude sont possibles chez ces alligators: on peut examiner le processus de formation de leurs rayures, ou bien le processus de formation des dents, qui est lui aussi intimement relié à la croissance de la mâchoire pendant le développement de l’embryon. Contrairement au cas des tâches sur le pelage des animaux, où c’est l’interaction entre le processus de réaction-diffusion et la forme de l’animal qui dictait la forme du motif final, c’est ici l’interaction entre le processus de réaction-diffusion et la dilatation de l’animal qui joue un rôle crucial. Comme pour les motifs des animaux, un système d’équations différentielles classique va décrire la formation des structures, mais ce système est obtenu après une transformation de l’espace qui prend en compte la croissance de l’embryon. Une fois résolu le système d’équations différentielles, on utilise la transformation inverse pour retrouver la solution sur le support croissant. Cliquer sur l’image pour lire la suite…

Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne une famille de méthodes algorithmiques visant à calculer une valeur numérique approchée en utilisant des procédés aléatoires, c’est-à-dire des techniques probabilistes. Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués à Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis, et publié pour la première fois en 1949 dans un article coécrit avec Stanislaw Ulam. Dans un premier temps, nous étudierons le principe de ces méthodes en fournissant deux estimateurs du nombre Pi. Le premier en lançant de manière aléatoire des points dans un quart de disque de rayon 1 inscrit dans un carré de côté 1. Le deuxième en lançant des segments de longueur l dans un réseau de droites parallèles distantes d’une longueur l. Dans un second temps, nous nous intéresserons à trois projets algorithmiques permettant de réinvestir et d’approfondir le principe de ces méthodes : en estimant une surface, en distinguant des caractères, en nous intéressant à la réduction de la variance par l’utilisation de variables antithétiques. Cliquer sur l’image pour lire la suite…

Un générateur de nombres pseudo-aléatoires, « pseudorandom number generator » (PRNG) en anglais, est un algorithme qui génère une séquence de nombres présentant certaines propriétés du hasard. Les nombres générés sont donc supposés être suffisamment indépendants les uns des autres, et aucune structure évidente ne doit apparaître… Pourquoi « pseudo-aléatoire » ? John von Neumann, est né le 28 décembre 1903 à Budapest et mort le 8 février 1957 à Washington, est un mathématicien et physicien américano-hongrois. On lui doit l’affirmation suivante : « Quiconque considère des méthodes arithmétiques pour produire des nombres aléatoires est, bien sûr, en train de commettre un péché ! ». Pourquoi en faire un sujet d’étude ? Donald Ervin Knut, né le 10 janvier 1938 à Milwaukee au Wisconsin, est un informaticien et mathématicien américain de renom, professeur émérite en informatique à l’université Stanford en tant que « professeur émérite de l’art de programmer ». On lui doit l’affirmation suivante : « Les générateurs de nombres aléatoires ne doivent pas être choisis au hasard ! ». Cliquer sur l’image pour lire la suite…
Les situations d’interactions sociales pour lesquelles on doit pouvoir faire confiance aux autres sont partie intégrante de notre vie quotidienne. Se fier à ses amis, se fier à ses enseignants, se fier aux membres de sa famille, aux vendeurs que l’on sollicite, aux politiciens que l’on écoute ainsi qu’à tous les membres de notre communauté est essentiel pour bien vivre en société. Toutefois, on observe de nombreuses situations où la coopération, qui pourrait porter à des résultats positifs pour la communauté dans son ensemble, est remplacée par l’égoïsme et l’égocentrisme des choix individuels. Dans un contexte de décision, la méfiance prend parfois le pas sur la confiance. Encourager la coopération est le but principal de plusieurs disciplines des sciences sociales comme l’économie, la psychologie, les sciences politiques. L’une de principales méthodes utilisées par ces disciplines est la théorie des jeux qui est un domaine des mathématiques qui étudie la prise de décision dans les situations d’interaction stratégiques, c’est-à-dire des situations où les individus doivent choisir en tenant compte des actions/réactions des autres individus et au-delà de leurs propres objectifs. Plusieurs modèles de la théorie des jeux offrent un cadre pour étudier l’évolution de la coopération et de la confiance. Nous nous intéresserons plus particulièrement au dilemme du prisonnier répété. Cliquer sur l’image pour lire la suite…



